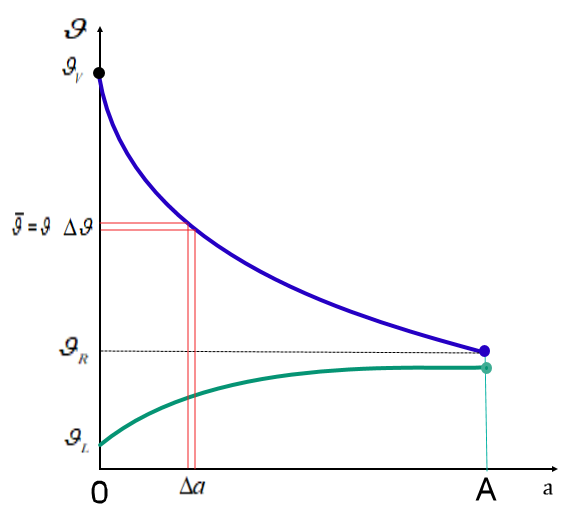
\[\begin{array}{*{20}{l}}{\bar \vartheta = \frac{1}{{\Delta a}} \cdot \int\limits_a^{a + \Delta a} {\vartheta \cdot da = } \frac{1}{{\Delta a}} \cdot \left( {F(a + \Delta a) - F(a)} \right)}\\{\mathop {\lim }\limits_{\Delta a \to 0} \frac{{F(a + \Delta s) - F(a)}}{{\Delta a}} = \frac{{dF}}{{da}} = \vartheta = \bar \vartheta }\end{array}\]
\[\begin{array}{l}\vartheta (a) = {c_1} + {c_2} \cdot {e^{ - {c_3} \cdot a}}\\\vartheta (0) = {c_1} + {c_2} = {\vartheta _V}\\\mathop {\lim }\limits_{a \to \infty } \vartheta (a) = {c_1} = {\vartheta _L}\end{array}\]
\[\vartheta (a) = {\vartheta _L} + \left( {{\vartheta _V} - {\vartheta _L}} \right) \cdot {e^{ - {c_3} \cdot a}}\]\[\left( {{\vartheta _V} - {\vartheta _L}} \right) \cdot {e^{ - {c_3} \cdot a}} = \vartheta - {\vartheta _L}\]\[d\vartheta = - {c_3} \cdot \left( {{\vartheta _V} - {\vartheta _L}} \right) \cdot {e^{ - {c_3} \cdot a}} \cdot da\]
\[\begin{array}{l}\dot Q = \dot m \cdot c \cdot \left( {{\vartheta _V} - \vartheta } \right) = U \cdot \left( {\bar \vartheta - {\vartheta _L}} \right) \cdot a\\d\dot Q = - \dot m \cdot c \cdot d\vartheta = U \cdot \left( {\bar \vartheta - {\vartheta _L}} \right) \cdot da\end{array}\]
In \[d\dot Q\] eingesetzt
\[\dot m \cdot c \cdot {c_3} \cdot \left( {{\vartheta _V} - {\vartheta _L}} \right) \cdot {e^{ - {c_3} \cdot a}} = U \cdot \left( {\bar \vartheta - {\vartheta _L}} \right)\]\[\left( {{\vartheta _V} - {\vartheta _L}} \right) \cdot {e^{ - {c_3} \cdot a}} = \vartheta - {\vartheta _L}\]\[\dot m \cdot c \cdot {c_3} \cdot \left( {\vartheta - {\vartheta _L}} \right) = U \cdot \left( {\bar \vartheta - {\vartheta _L}} \right)\]\[\dot m \cdot c \cdot {c_3} = U \leftrightarrow {c_3} = \frac{U}{{\dot m \cdot c}}\]\[\begin{array}{l}\vartheta - {\vartheta _L} = \bar \vartheta - {\vartheta _L}\\\vartheta = \bar \vartheta \end{array}\]\[\vartheta \left( a \right) = {\vartheta _L} + \left( {{\vartheta _V} - {\vartheta _L}} \right) \cdot {e^{ - \frac{{U \cdot a}}{{\dot m \cdot c}}}}\]
\[\vartheta \left( a \right) = {\vartheta _L} + \left( {{\vartheta _V} - {\vartheta _L}} \right) \cdot {e^{ - \frac{{U \cdot a}}{{\dot m \cdot c}}}}\]