Eine Kaskade vieler kleiner Heizkörper ergibt in der Summe einen großen Heizkörper. Die Rücklauftemperaturen werden in Abhängigkeit der aufsummierten Heizkörperflächen in einem Diagramm dargestellt.
Eine Kaskade vieler kleiner Heizkörper ergibt in der Summe einen großen Heizkörper. Die Rücklauftemperaturen werden in Abhängigkeit der aufsummierten Heizkörperflächen in einem Diagramm dargestellt.
\[\begin{array}{*{20}{l}}{\bar \vartheta = \frac{1}{{\Delta a}} \cdot \int\limits_a^{a + \Delta a} {\vartheta \cdot da = } \frac{1}{{\Delta a}} \cdot \left( {F(a + \Delta a) - F(a)} \right)}\\{\mathop {\lim }\limits_{\Delta a \to 0} \frac{{F(a + \Delta s) - F(a)}}{{\Delta a}} = \frac{{dF}}{{da}} = \vartheta = \bar \vartheta }\end{array}\]
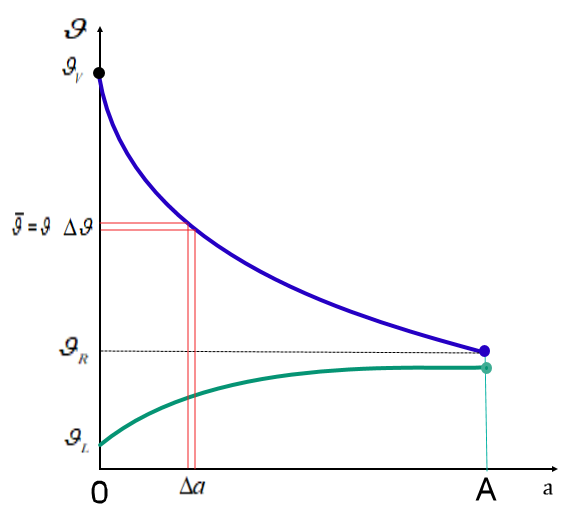
| \[{\vartheta _V}\] | Vorlauftemperatur |
| \[\vartheta \] | Rücklauftemperatur variabel (blau) |
| \[\bar \vartheta \] | mittlere Temperatur (Vor- und Rücklauf) |
| \[{\vartheta _R}\] | Rücklauftemperatur |
| \[{\vartheta _L}\] | Umgebungstemperatur (grün) |
| A | Heizkörperfläche |
| a | Heizkörperfläche variabel |
\[\begin{array}{l}\dot Q(\dot m,\vartheta ,\bar \vartheta ,{\vartheta _L},A)\\d\dot Q = \frac{{\partial \dot Q}}{{\partial \dot m}}d\dot m + \frac{{\partial \dot Q}}{{\partial \vartheta }}d\vartheta + \frac{{\partial \dot Q}}{{\partial \bar \vartheta }}d\bar \vartheta + \frac{{\partial \dot Q}}{{\partial {\vartheta _L}}}d{\vartheta _L} + \frac{{\partial \dot Q}}{{\partial a}}da\end{array}\]
\[\begin{array}{l}{\rm{Ansatz:}}\\\dot Q = \dot m \cdot c \cdot ({\vartheta _V} - \vartheta ) = U \cdot (\bar \vartheta - {\vartheta _L}) \cdot a\\\frac{{d\dot Q}}{{da}} = \dot m \cdot c \cdot ( - \frac{{d\vartheta }}{{da}}) = U \cdot (\bar \vartheta - {\vartheta _L}) \cdot \frac{{da}}{{da}}\\\\\bar \vartheta = \mathop {\lim }\limits_{\Delta \vartheta \to 0} \frac{1}{2}((\vartheta + \frac{1}{2}\Delta \vartheta ) + (\vartheta - \frac{1}{2}\Delta \vartheta )) = \vartheta \\\\d\dot Q = - \dot m \cdot c \cdot d\vartheta = U \cdot (\vartheta - {\vartheta _L}) \cdot da\\\int\limits_{{\vartheta _V}}^\vartheta {\frac{{d\vartheta }}{{\vartheta - {\vartheta _L}}} = - \frac{U}{{\dot m \cdot c}}\int\limits_0^a {da} } \\\\\vartheta = {\vartheta _L} + ({\vartheta _V} - {\vartheta _L}) \cdot {e^{ - \frac{{U \cdot a}}{{\dot m \cdot c}}}}\\\\{\rm{Massenstrom}}\,\,{\rm{\dot m }}\,{\rm{ist}}\,\,{\rm{unveraendert}}\\a = 0 \Rightarrow \vartheta = {\vartheta _V}\\a = A \Rightarrow \vartheta = {\vartheta _R}\\\\{\rm{Flaeche}}\,\,{\rm{A }}\,\,{\rm{ist }}\,\,{\rm{unveraendert}}\\\dot m = 0 \Rightarrow \vartheta = {\vartheta _R} = {\vartheta _L}\\\dot m \to \infty \Rightarrow \vartheta \to {\vartheta _V}\end{array}\]
Durch Umformen der Gleichung
\[\dot Q(\vartheta ) = \dot m \cdot c \cdot ({\vartheta _V} - \vartheta ) = A \cdot U \cdot {\left( {\frac{{{\vartheta _V} - \vartheta }}{{\ln (\frac{{{\vartheta _V} - {\vartheta _L}}}{{\vartheta - {\vartheta _L}}})}}} \right)^n}\]
nach der Temperatur ergibt sich denn wieder für n = 1 die gesuchte Gleichung.
Wegen des Wärmeüberganges ist der U-Wert ist ebenfalls von der Strömungsgeschwindigkeit (Massenstrom) abhängig; allerdings wird dieser in den Berechnungen als Konstante angenommen.
\[\dot Q(\vartheta ) = \dot m \cdot c \cdot ({\vartheta _V} - \vartheta ) = A \cdot U \cdot {\left( {\frac{{{\vartheta _V} - \vartheta }}{{\ln (\frac{{{\vartheta _V} - {\vartheta _L}}}{{\vartheta - {\vartheta _L}}})}}} \right)^n}\]
\[{\vartheta _V} = 75^\circ C\,\,\,{\vartheta _L} = 20^\circ C\,\,\,c = \frac{{W \cdot h}}{{kg \cdot K}}\,\,\,\,U\,in\,\frac{W}{{{m^2} \cdot {K^n}}}\,\,\,n = 1,3\,\,\,\dot m = 50\frac{{kg}}{h}\,\,A = 1{m^2}\]
| \[{\dot m}\] in kg/h |
\[\vartheta \] in °C (genau) |
\[\vartheta \] in °C (berechnet nach Gl. 1) |
|---|---|---|
| 15 | 20,2 | 20,6 |
| 20 | 20,6 | 21,2 |
| 25 | 21,2 | 22 |
| 50 | 26,2 | 27 |
| 100 | 36,3 | 36,7 |
| 500 | 61,8 | 61,8 |
| 1000 | 67,8 | 67,8 |
| 2000 | 71,2 | 71,2 |
| 3000 | 72,5 | 72,5 |
| 5000 | 73,5 | 73,5 |
