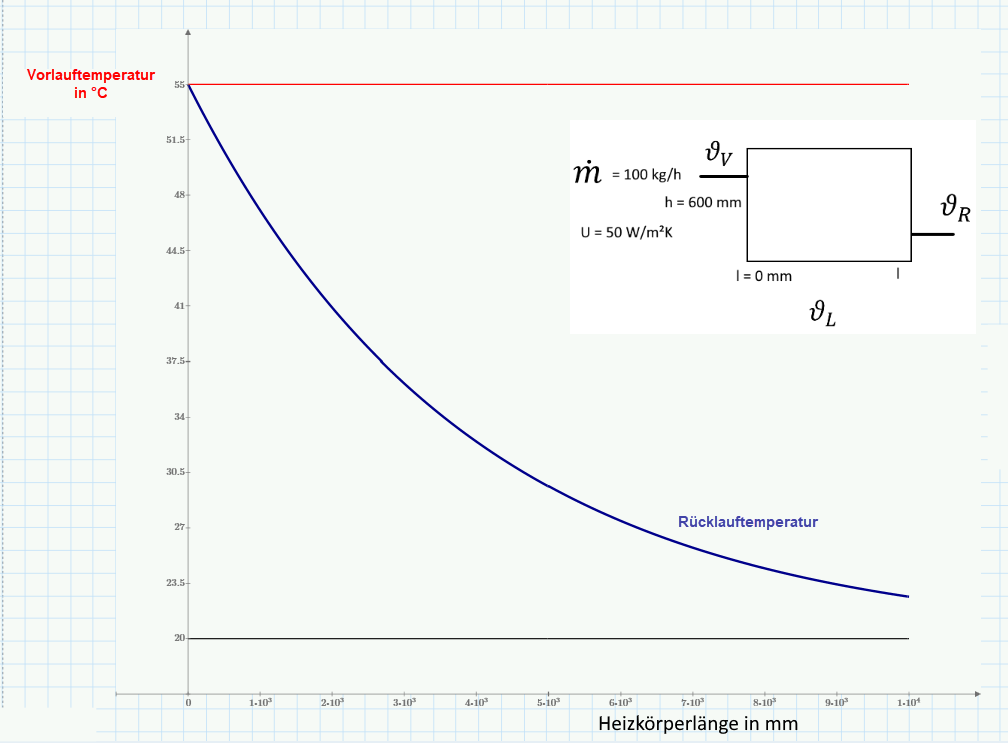
Heizkörperleistung und Übertemperatur

A Heizkörperfläche (Bild 1)

Abkühlkurve

\[\begin{array}{l}{\rm{mittlere\_Uebertemperatur}}\\\Delta {\vartheta _m} = \bar \vartheta - {\vartheta _L} = \frac{{{\vartheta _V} + {\vartheta _R}}}{2} - {\vartheta _L}\\\\{\rm{logarithmische\_Uebertemperatur}}\\\Delta {\vartheta _m} = \frac{{{\vartheta _V} - {\vartheta _R}}}{{\ln (\frac{{{\vartheta _V} - {\vartheta _L}}}{{{\vartheta _R} - {\vartheta _L}}})}}\end{array}\]

HeizkörperexponentUmrechnungsfaktor
    1. Geben Sie die Systemtemperaturen (Bild 1) an.
    2. Geben Sie den Umrechnungsfaktor an.
    3. Erklären Sie den Begriff Umrechnungsfaktor.
    4. Beschreiben Sie den Begriff Übertemperatur.
    5. Geben Sie die Übertemperatur an. (linear und logarithmisch)
    6. Was bedeutet es, wenn die Übertemperatur bei gleichbleibender Vorlauftemperatur kleiner wird?
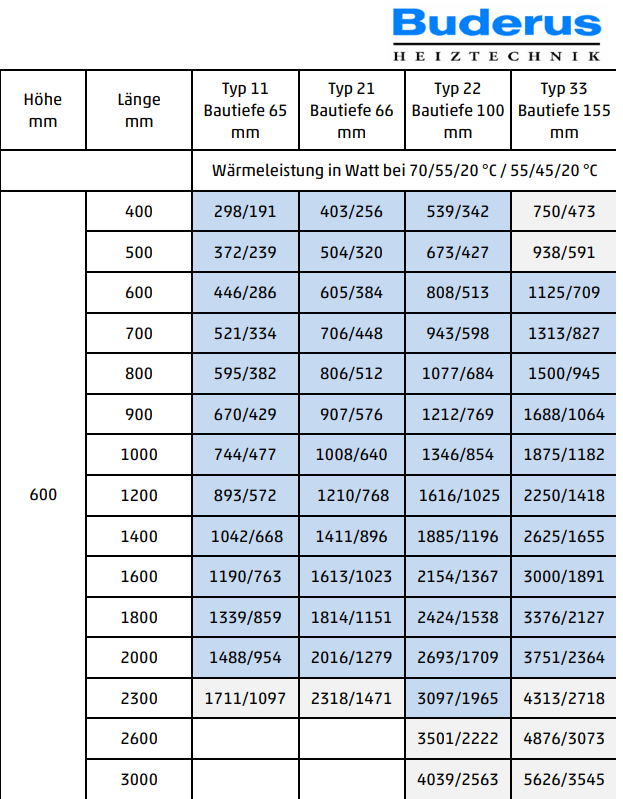
    1. Wie groß ist die Heizleistung? (Buderus Tabelle (55/45/20), Typ 22, Länge = 900 mm.
    2. Geben Sie die Gleichungen für den Massenstrom, Volumenstrom und der Strömungsgeschwindigkeit an.
    3. Geben Sie den Massenstrom an.
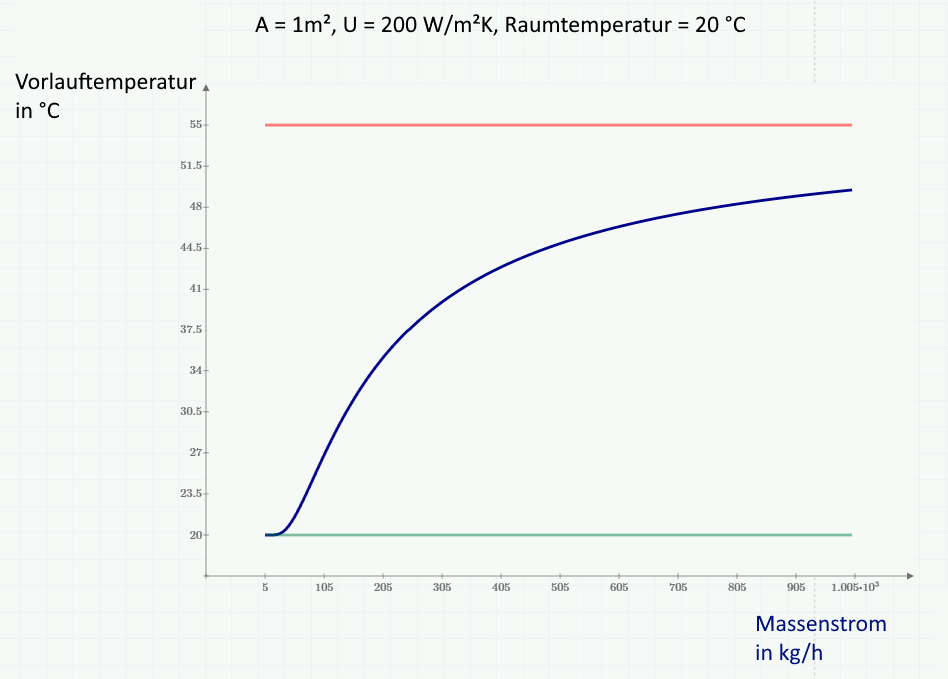
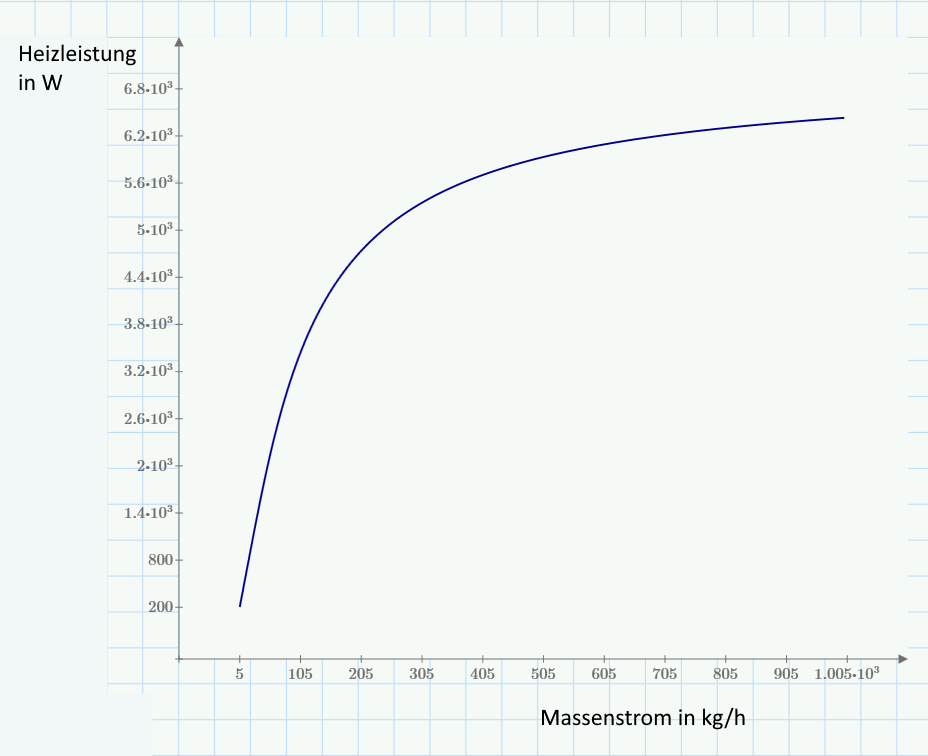
    4. Beschreiben Sie den Zusammenhang zwischen Massenstrom und Heizleistung. Sind sehr große Massenströme sinnvoll?
  3. Von welcher Größe ist die Entscheidung abhängig, ob mit der linearen Übertemperatur gerechnet werden kann?
  4. Zeichnen Sie ein Diagramm für die lineare Übertemperatur (Bild 2) in dem die Heizleistung (Wärmestrom) in Abhängigkeit der Heizkörperfläche gezeigt wird. (x-Achse: Heizkörperfläche a, y-Achse: Wärmestrom)

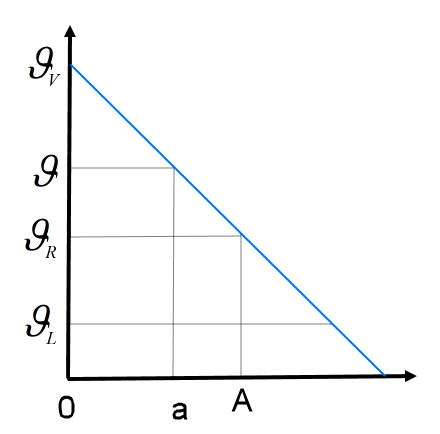
    Bild 2

  5. Geben Sie die Temperaturdifferenzen (Bild 1) für folgende Wämeströme an:
    1. im Heizkörper
    2. Heizkörper - Raum
    3. Raum - Außen
Kontakt