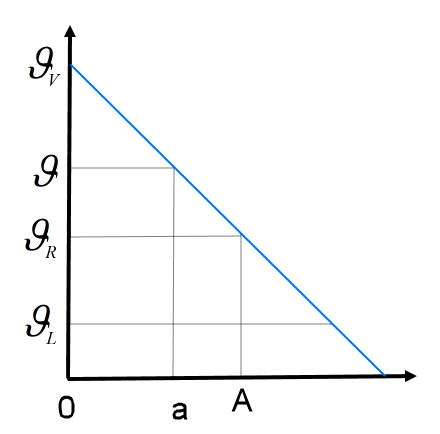
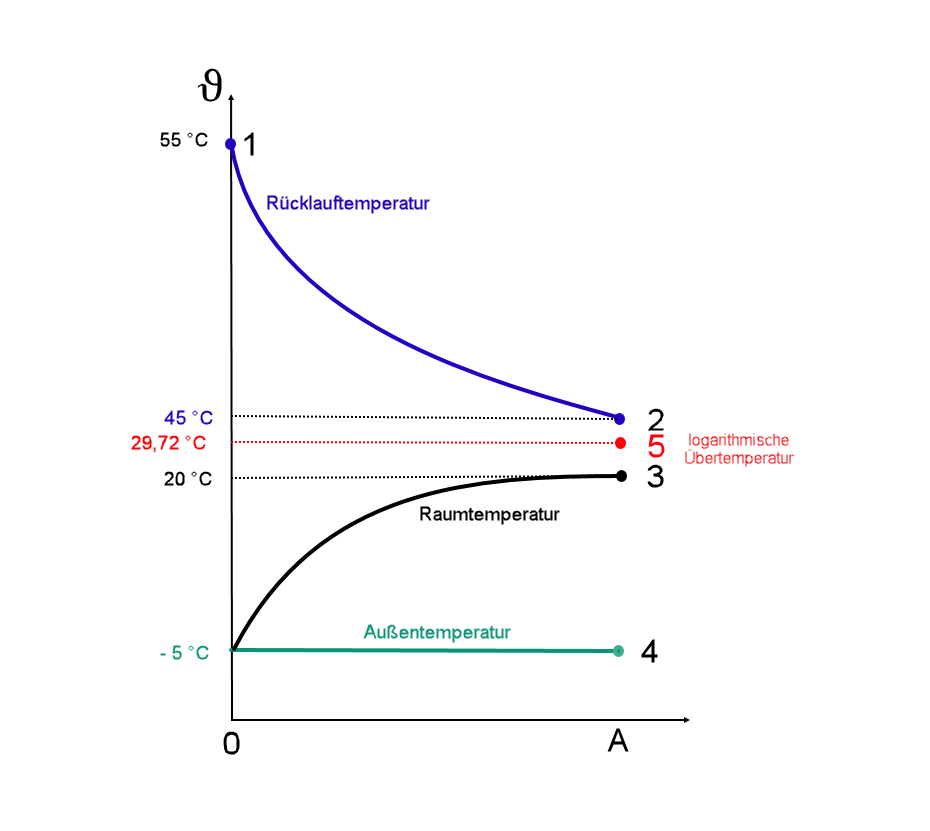
\[\begin{array}{l}\frac{{{\vartheta _V} - {\vartheta _R}}}{A} = \frac{{{\vartheta _V} - \vartheta }}{a} \leftrightarrow \vartheta = {\vartheta _V} - \frac{{{\vartheta _V} - {\vartheta _R}}}{A} \cdot a\\\bar \vartheta = \frac{1}{A}\int\limits_0^A {\vartheta \cdot da} \to \bar \vartheta = \frac{{{\vartheta _V} + {\vartheta _R}}}{2}\\\Delta {\vartheta _m} = \bar \vartheta - {\vartheta _L} \to \Delta {\vartheta _m} = \frac{{{\vartheta _V} + {\vartheta _R}}}{2} - {\vartheta _L}\end{array}\]
A = Heizkörperfläche

\[\begin{array}{l}\vartheta (l) = {\vartheta _V} - \frac{l}{L} \cdot \left( {{\vartheta _V} - {\vartheta _R}} \right)\\\dot Q = \dot m \cdot c \cdot \left( {{\vartheta _V} - \vartheta (l)} \right)\\\dot Q = \dot m \cdot c \cdot \left( {{\vartheta _V} - \left( {{\vartheta _V} - \frac{l}{L} \cdot \left( {{\vartheta _V} - {\vartheta _R}} \right)} \right)} \right)\\\dot Q = \dot m \cdot c \cdot \frac{l}{L} \cdot \left( {{\vartheta _V} - {\vartheta _R}} \right)\end{array}\]

\[\begin{array}{l}{\rm{Ansatz:}}{\mkern 1mu} {\mkern 1mu} \,d\dot Q = - \dot m \cdot c \cdot d\vartheta = U \cdot (\vartheta - {\vartheta _L}) \cdot da\\\int\limits_{{\vartheta _V}}^{{\vartheta _R}} {\frac{{d\vartheta }}{{\vartheta - {\vartheta _L}}} = - \frac{U}{{\dot m \cdot c}}\int\limits_0^A {da} } \\\ln (\frac{{{\vartheta _R} - {\vartheta _L}}}{{{\vartheta _V} - {\vartheta _L}}}) = - \frac{{U \cdot A}}{{\dot m \cdot c}}\, \leftrightarrow \,(\frac{{{\vartheta _R} - {\vartheta _L}}}{{{\vartheta _V} - {\vartheta _L}}}) = {e^{ - \frac{{U \cdot A}}{{\dot m \cdot c}}}}\\\vartheta = {\vartheta _L} + ({\vartheta _V} - {\vartheta _L}) \cdot {e^{ - \frac{{U \cdot a}}{{\dot m \cdot c}}}}\\\Delta {\vartheta _m} = \bar \vartheta - {\vartheta _L}\\\bar \vartheta = \frac{1}{A} \cdot \int\limits_0^A {\vartheta \cdot da} \,{\mkern 1mu} \\\bar \vartheta = \frac{1}{A} \cdot ({\vartheta _L} \cdot A + ({\vartheta _V} - {\vartheta _L}) \cdot ( - \frac{1}{{\frac{U}{{\dot m \cdot c}}}}) \cdot ({e^{ - \frac{{U \cdot A}}{{\dot m \cdot c}}}} - 1))\\\bar \vartheta = \frac{1}{A} \cdot ({\vartheta _L} \cdot A + ({\vartheta _V} - {\vartheta _L}) \cdot \frac{A}{{\ln (\frac{{{\vartheta _R} - {\vartheta _L}}}{{{\vartheta _V} - {\vartheta _L}}})}} \cdot (\frac{{{\vartheta _R} - {\vartheta _L}}}{{{\vartheta _V} - {\vartheta _L}}} - 1))\\\bar \vartheta = ({\vartheta _L} + ({\vartheta _V} - {\vartheta _L}) \cdot \frac{1}{{\ln (\frac{{{\vartheta _R} - {\vartheta _L}}}{{{\vartheta _V} - {\vartheta _L}}})}} \cdot (\frac{{{\vartheta _R} - {\vartheta _V}}}{{{\vartheta _V} - {\vartheta _L}}}))\\\Delta {\vartheta _m} = \frac{{{\vartheta _V} - {\vartheta _R}}}{{\ln (\frac{{{\vartheta _V} - {\vartheta _L}}}{{{\vartheta _R} - {\vartheta _L}}})}}\end{array}\]

Das Diagramm zeigt die prozentuale Abweichung zwischen der logarithmischen (100 %) und linearen Übertemperatur.
Bei einer Abweichung von 5 % beträgt die Temperaturspreizung 30 K (°C).
In diesem Beispiel könnte man bis 30 K auch mit der linearen Übertemperatur rechnen, ohne das der Fehler zu groß wird.