\[\begin{array}{l}\vartheta (\dot m) = {c_1} + {c_2} \cdot {e^{ - \frac{{{c_3}}}{{\dot m}}}}\\\dot m = 0 \to \vartheta (\dot m = 0) = {\vartheta _{R0}} = {c_1}\\\mathop {\lim }\limits_{\dot m \to \infty } \left( {{c_1} + {c_2} \cdot {e^{ - \frac{{{c_3}}}{{\dot m}}}}} \right) \to \vartheta (\dot m) = {\vartheta _V} = {c_1} + {c_2}\\\vartheta (\dot m) = {\vartheta _{R0}} + \left( {{\vartheta _V} - {\vartheta _{R0}}} \right) \cdot {e^{ - \frac{{{c_3}}}{{\dot m}}}}\\\dot Q = \dot m \cdot c \cdot \left( {{\vartheta _V} - \vartheta (\dot m)} \right)\end{array}\]

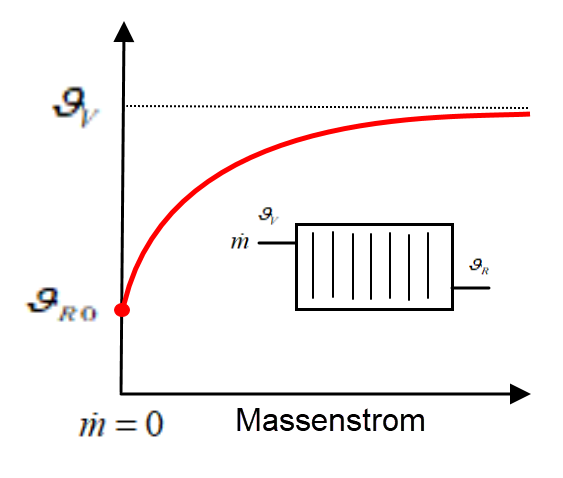
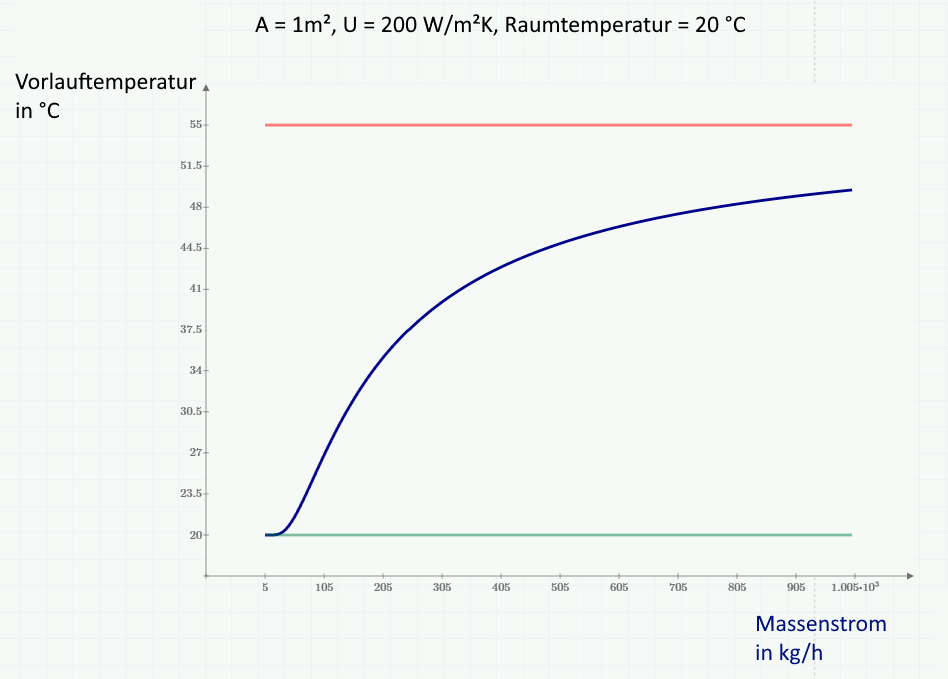
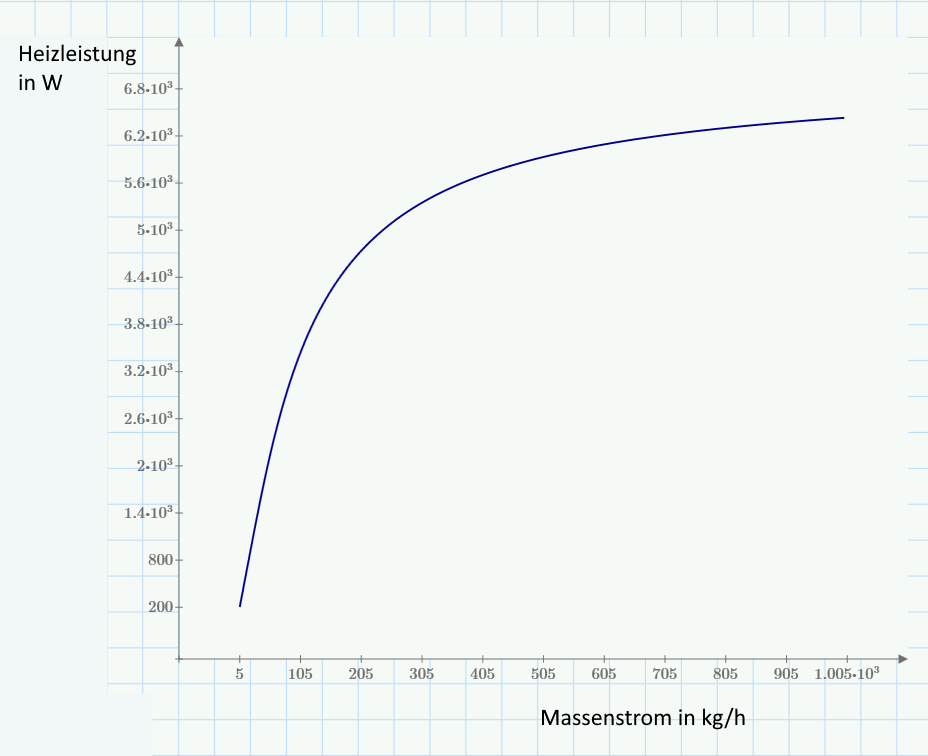
Der Wärmeübergangskoeffizient \[\alpha \] ist von der Strömungsgeschwindigkeit (Massenstrom) abhängig. Steigt der Massenstrom, nimmt auch der Wärmestrom zu.